A cikk eredeti címe: 14C age of recent natural earthworm biospheroids ̶ implications for paleosol dating
A talajképződés és a talajban zajló szénfolyamatok vizsgálata alapvető fontosságú a globális környezeti változások megértéséhez. A talajfejlődési folyamatok időbeli lefolyásának, vagyis a „talajkor” meghatározása azonban mindmáig jelentős kihívást jelent a földtudományok számára. A talaj egy folyamatosan képződő/alakuló, komplex rendszer, amelyben a szerves szénfrakciók eltérő eredetű és korú komponenseket tartalmazhatnak, a frissen beépült növényi maradványoktól egészen a több ezer éves, stabilizálódott humuszfrakciókig. A szervesanyag alapú radiokarbon kormeghatározás ezért a talajok esetében gyakran korlátozottan alkalmazható. A mérésekhez többféle anyag használható, például a teljes szerves szén, annak egyes frakciói, illetve makrofosszíliák, mint a faszén, növényi törmelék, csigák vagy kagylók. Ezek azonban nem minden esetben in situ, az adott talajrétegben keletkeztek, így a mért radiokarbon kor nem feltétlenül tükrözi a talajképződési esemény tényleges idejét.
Kutatásunk a talajban képződő másodlagos karbonátok egy különleges típusára, a földigiliszták (Lumbricidae család) által kiválasztott kalcium-karbonát bioszferoidokra irányult, amelyek új lehetőséget kínálnak a talajkronológiai vizsgálatokhoz a radiokarbonos datálás területén. Ezek a néhány milliméter (0,5-1 mm) átmérőjű kalcitgömbök a földigiliszták Morren-féle mészmirigyeiben képződnek, majd kiválasztásuk után a talajban stabilan megőrzik a keletkezésük idején uralkodó szénizotópos összetételt.
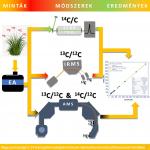
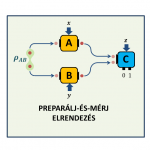
A vizsgálatokhoz Debrecen környéki, csernozjom talajokból gyűjtöttünk természetes, recens bioszferoidokat. A minták előkészítése és a radiokarbon (14C) mérések a debreceni HEKAL laboratóriumban, gyorsítós tömegspektrometriás (AMS), gázionforrásos (GIS) méréstechnikát alkalmazva történtek.
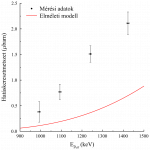
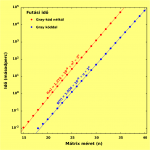
A földigiliszta bioszferoidokból mért 14C-aktivitások a mintavétel idején érvényes légköri értékekkel egyezőnek bizonyultak, azaz a bennük megkötött szén rendkívül fiatal, biogén eredetű, és közvetlenül a talaj–légkör közötti aktív szénáramláshoz kapcsolódik, nem pedig a talajban hosszabb ideig tárolt, idősebb szénkészletből származik.
A tanulmányban az első hazai kísérletsorozat eredményeit mutatjuk be, amely során igazoltuk, hogy ezek a biogén, kalcium-karbonátos eredetű bioszferoidok alkalmasak a recens talajfolyamatok radiokarbonos vizsgálatára, és megbízhatóan közvetítik a légköri/biológiai szénizotópos jelet. Az első hazai földigiliszta bioszferoidokon végzett radiokarbonos kísérletsorozat igazolta a módszer gyakorlati alkalmazhatóságát, és perspektivikus irányt nyit az idős (pleisztocén-holocén), eltemetett paleotalajok és löszrétegek kronológiai vizsgálatában.


 English
English
